重要思想：积分

写在前面的前面

积分、极限、导数，这三个有的时候是可以同时出现的，那么积分是什么呢？

写在前面

类似于极限那一章我们提到的关于切割圆的例子，也是微积分思想，再次就不再赘述了，我们直奔主题！

引入

我们都知道长方形、平行四边形、三角形等等图形的面积公式，哪怕是多边形我们也可以根据辅助线求出面积，但是，这些都是方方正正有棱有角的图形，如果我让你求一个圆弧与其他线构成的图形的面积，你又该怎么求？假设是一个二次函数与 $x$ 轴围成的面积，怎么去算？

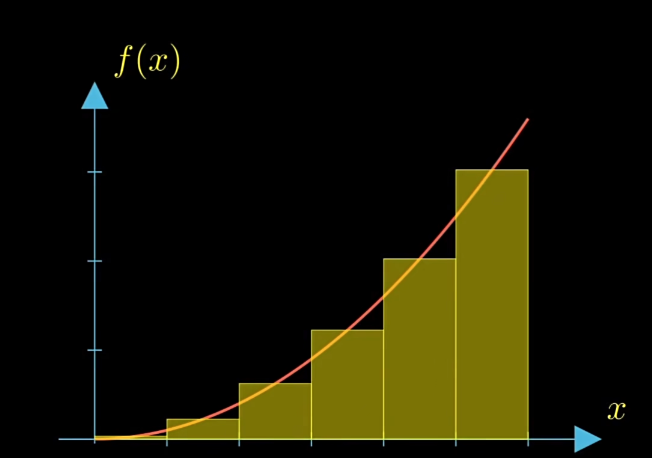
我们像这样，用几个长方形将面积等分，每个长方形的高为它们的顶边与图像的焦点横坐标。于是，我们把长方形拿出来进行观察，把它的宽叫做 $dx$，随着 $dx$ 的减小，无限趋于 $0$ 的时候，所有的长方形刚好可以填满整个所要求的面积，至此，我们完成了微分的过程。接下来只需要计算出长方形的面积之和就可以了。

公式 / 牛顿莱布尼茨公式

我们利用导函数和原函数之间的关系，即 $f(x)\to F(x)$，可以得到：

$$F(b)-F(a)=\int^b_a f(x) dx$$

那么在本题目中我们先要找到原函数。

$$f(x)=x^2\to F(x)=\frac{1}{3}x^3+C$$

根据公式可以求出面积：

$$\int^6_0 f(x)dx=F(6)-F(0)=72$$

因此原题目中的面积为 $\boxed{72}$。

详细的推导过程

我们可以把上面的公式进行推导，假设我们要计算 $f(x)$ 在 $[a,b]$ 上的定积分，我们可以把它分成 $n$ 个小区间，每个小区间的宽度为 $\Delta x=\frac{b-a}{n}$，每个小区间的左端点为 $x_i=a+i\Delta x$，那么我们就可以得到：

$$\int_a^b f(x)dx=\lim_{n\to\infty}\sum_{i=1}^n f(x_i)\Delta x$$

然后，我们可以把 $\Delta x$ 代入上面的公式，得到：

$$\int_a^b f(x)dx=\lim_{n\to\infty}\sum_{i=1}^n f(a+i\Delta x)\cdot \frac{b-a}{n}$$

化简，得到：

$$\int_a^b f(x)dx=\lim_{n\to\infty}\frac{b-a}{n}\sum_{i=1}^n f(a+i\Delta x)$$

于是：

$$\int_a^b f(x)dx=\lim_{n\to\infty}\frac{b-a}{n}\sum_{i=1}^n f(a+i\frac{b-a}{n})$$

最后，我们可以把上面的公式进行化简，得到：

$$\int_a^b f(x)dx=\lim_{n\to\infty}\frac{b-a}{n}\sum_{i=1}^n f(a+i\frac{b-a}{n})=\int_a^b f(x)dx$$

---

我都看不懂，再见了。