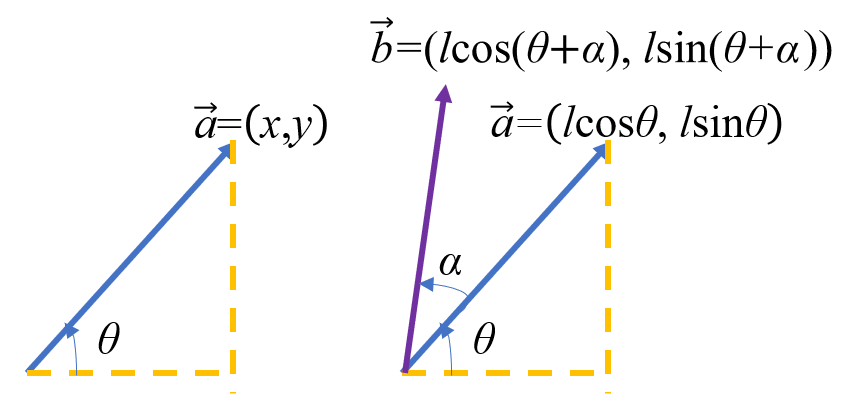跳到主要内容

向量

在本文之前，特别说明一下翻译的相关问题。由于历史原因，数学学科和物理学科关于「vector」一词的翻译不同。

在物理学科，一般翻译成「矢量」，并且与「标量」一词相对。在数学学科，一般翻译成「向量」。这种翻译的差别还有「本征」与「特征」、「幺正」与「酉」，等等。

定义及相关概念​

向量：既有大小又有方向的量称为向量。数学上研究的向量为 自由向量，即只要不改变它的大小和方向，起点和终点可以任意平行移动的向量。记作 a⃗\vec a 或 a\boldsymbol{a}。

有向线段：带有方向的线段称为有向线段。有向线段有三要素：起点，方向，长度，知道了三要素，终点就唯一确定。一般使用有向线段表示向量。

向量的模：有向线段 AB→\overrightarrow{AB} 的长度称为向量的模，即为这个向量的大小。记为：∣AB→∣|\overrightarrow{AB}| 或 ∣a∣|\boldsymbol{a}|。

零向量：模为 00 的向量。零向量的方向任意。记为：0⃗\vec 0 或 0\boldsymbol{0}。

单位向量：模为 11 的向量称为该方向上的单位向量。一般记为 e⃗\vec e 或 e\boldsymbol{e}。

平行向量：方向相同或相反的两个 非零 向量。记作：a∥b\boldsymbol a\parallel \boldsymbol b。对于多个互相平行的向量，可以任作一条直线与这些向量平行，那么任一组平行向量都可以平移到同一直线上，所以平行向量又叫 共线向量。

相等向量：模相等且方向相同的向量。

相反向量：模相等且方向相反的向量。

向量的夹角：已知两个非零向量 a,b\boldsymbol a,\boldsymbol b，作 OA→=a,OB→=b\overrightarrow{OA}=\boldsymbol a,\overrightarrow{OB}=\boldsymbol b，那么 θ=∠AOB\theta=\angle AOB 就是向量 a\boldsymbol a 与向量 b\boldsymbol b 的夹角。记作：⟨a,b⟩\langle \boldsymbol a,\boldsymbol b\rangle。显然当 θ=0\theta=0 时两向量同向，θ=π\theta=\pi 时两向量反向，θ=π2\theta=\frac{\pi}{2} 时两向量垂直，记作 a⊥b\boldsymbol a\perp \boldsymbol b，并且规定 θ∈[0,π]\theta \in [0,\pi]。

注意到平面向量具有方向性，两个向量不能比较大小（但可以比较两向量的模长）。但是两个向量可以相等。

向量的线性运算​

向量的加减法​

在定义了一种量之后，就希望让它具有运算。向量的运算可以类比数的运算，从物理学的角度出发也可以研究向量的运算。

类比物理学中的位移概念，假如一个人从 AA 经 BB 走到 CC，那么他经过的位移为 AB→+BC→\overrightarrow{AB}+\overrightarrow{BC}，这其实等价于这个人直接从 AA 走到 CC，即 AB→+BC→=AC→\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}。

注意到力的合成法则——平行四边形法则，同样也可以看做一些向量相加。

整理一下向量的加法法则：

  1. 向量加法的三角形法则：若要求和的向量首尾顺次相连，那么这些向量的和为第一个向量的起点指向最后一个向量的终点；
  2. 向量加法的平行四边形法则：若要求和的两个向量 共起点，那么它们的和向量为以这两个向量为邻边的平行四边形的对角线，起点为两个向量共有的起点，方向沿平行四边形对角线方向。

这样，向量的加法就具有了几何意义。并且可以验证，向量的加法满足 交换律与结合律。

因为实数的减法可以写成加上相反数的形式，考虑在向量做减法时也这么写。即：a−b=a+(−b)\boldsymbol a-\boldsymbol b=\boldsymbol a+(-\boldsymbol b)。

这样，考虑共起点的向量，按照平行四边形法则做出它们的差，经过平移后可以发现 「共起点向量的差向量」是由「减向量」指向「被减向量」的有向线段。这也是向量减法的几何意义。

有时候有两点 A,BA,B，想知道 AB→\overrightarrow{AB}，可以利用减法运算 AB→=OB→−OA→\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA} 获得。

向量的数乘​

规定「实数 λ\lambda 与向量 a\boldsymbol a 的积」为一个向量，这种运算就是向量的 数乘运算，记作 λa\lambda \boldsymbol a，它的长度与方向规定如下：

  1. ∣λa∣=∣λ∣∣a∣|\lambda \boldsymbol a|=|\lambda||\boldsymbol a|；
  2. 当 λ>0\lambda >0 时，λa\lambda\boldsymbol a 与 a\boldsymbol a 同向，当 λ=0\lambda =0 时，λa=0\lambda \boldsymbol a=\boldsymbol 0，当 λ<0\lambda<0 时，λa\lambda \boldsymbol a 与 a\boldsymbol a 方向相反。

根据数乘的定义，可以验证有如下运算律：

λ(μa)=(λμ)a(λ+μ)a=λa+μaλ(a+b)=λa+λb\begin{aligned} \lambda(\mu \boldsymbol a)&=(\lambda \mu)\boldsymbol a\\ (\lambda+\mu)\boldsymbol a&=\lambda \boldsymbol a+\mu \boldsymbol a\\ \lambda(\boldsymbol a+\boldsymbol b)&=\lambda \boldsymbol a+\lambda \boldsymbol b \end{aligned}

特别地：

(−λ)a=−(λa)=−λ(a)λ(a−b)=λa−λb\begin{gathered} (-\lambda)\boldsymbol a=-(\lambda \boldsymbol a)=-\lambda(\boldsymbol a)\\ \lambda(\boldsymbol a-\boldsymbol b)=\lambda \boldsymbol a-\lambda \boldsymbol b \end{gathered}

判定两向量共线​

两个 非零 向量 a\boldsymbol a 与 b\boldsymbol b 共线   ⟺  \iff 有唯一实数 λ\lambda，使得 b=λa\boldsymbol b=\lambda \boldsymbol a。

证明：由数乘的定义可知，对于 非零 向量 a\boldsymbol a，如果存在实数 λ\lambda，使得 b=λa\boldsymbol b=\lambda \boldsymbol a，那么 a∥b\boldsymbol a \parallel \boldsymbol b。

反过来，如果 a∥b\boldsymbol a\parallel \boldsymbol b，a≠0\boldsymbol a \not = \boldsymbol 0，且 ∣b∣=μ∣a∣|\boldsymbol b|=\mu |\boldsymbol a|，那么当 a\boldsymbol a 与 b\boldsymbol b 同向时，b=μa\boldsymbol b=\mu \boldsymbol a，反向时 b=−μa\boldsymbol b=-\mu \boldsymbol a。

最后，向量的加，减，数乘统称为向量的线性运算。

平面向量的基本定理及坐标表示​

平面向量基本定理​

定理内容：如果两个向量 e1,e2\boldsymbol{e_1},\boldsymbol{e_2} 不共线，那么存在唯一实数对 (x,y)(x,y)，使得与 e1,e2\boldsymbol{e_1},\boldsymbol{e_2} 共面的任意向量 p\boldsymbol p 满足 p=xe1+ye2\mathbf p=x\boldsymbol{e_1}+y\boldsymbol{e_2}。

平面向量那么多，怎样用尽可能少的量表示出所有平面向量？

只用一个向量表示出所有向量显然是不可能的，最多只能表示出某条直线上的向量。

再加入一个向量，用两个 不共线 向量表示（两个共线向量在此可以看成同一个向量），这样可以把任意一个平面向量分解到这两个向量的方向上了。

在同一平面内的两个不共线的向量称为 基底。如果基底相互垂直，那么在分解的时候就是对向量 正交分解。

平面向量的坐标表示​

如果取与横轴与纵轴方向相同的单位向量 i,ji,j 作为一组基底，根据平面向量基本定理，平面上的所有向量与有序实数对 (x,y)(x,y) 一一对应。

而有序实数对 (x,y)(x,y) 与平面直角坐标系上的点一一对应，于是作 OP→=p\overrightarrow{OP}=\boldsymbol p，那么终点 P(x,y)P(x,y) 也是唯一确定的。由于研究的对象是自由向量，可以自由平移起点，这样，在平面直角坐标系里，每一个向量都可以用有序实数对唯一表示。

平面向量的坐标运算​

平面向量线性运算​

由平面向量的线性运算可以推导其坐标运算，主要方法是将坐标全部化为用基底表示，然后利用运算律进行合并，之后表示出运算结果的坐标形式。

若两向量 a=(m,n)\boldsymbol a=(m,n)，b=(p,q)\boldsymbol b=(p,q)，则：

a+b=(m+p,n+q)a−b=(m−p,n−q)ka=(km,kn)\begin{aligned} \boldsymbol a+\boldsymbol b&=(m+p,n+q)\\ \boldsymbol a-\boldsymbol b&=(m-p,n-q)\\ k\boldsymbol a&=(km,kn) \end{aligned}

求一个向量的坐标表示​

已知两点 A(a,b),B(c,d)A(a,b),B(c,d)，易证 AB→=(c−a,d−b)\overrightarrow{AB}=(c-a,d-b)。

平移一点​

有时需要将一个点 PP 沿一定方向平移某单位长度，这样把要平移的方向和距离组合成一个向量，利用向量加法的三角形法则，将 OP→\overrightarrow{OP} 加上这个向量，得到的向量终点即为平移后的点。

三点共线的判定​

若 A,B,CA,B,C 三点共线，则 OB→=λOA→+(1−λ)OC→\overrightarrow{OB}=\lambda \overrightarrow{OA}+(1-\lambda)\overrightarrow{OC}。

三点共线判定的拓展​

在三角形 ABCABC 中，若 DD 为 BCBC 的 nn 等分点（n BD=k DCn\ BD=k\ DC），则有：AD→=nk+nAB→+kk+nAC→\overrightarrow{AD}=\frac{n}{k+n}\overrightarrow{AB}+\frac{k}{k+n}\overrightarrow{AC}

在三维空间中的拓展（立体几何/空间向量）​

在空间中，以上部分所述的所有内容均成立。更有：

空间向量基本定理​

定理内容：如果三个向量 e1,e2,e3\boldsymbol{e_1},\boldsymbol{e_2},\boldsymbol{e_3} 不共面，那么存在唯一实数对 (x,y,z)(x,y,z)，使得空间中任意向量 p\boldsymbol p 满足 p=xe1+ye2+ze3\mathbf p=x\boldsymbol{e_1}+y\boldsymbol{e_2}+z\boldsymbol{e_3}。 根据空间向量基本定理，我们同样可以使用三个相互垂直的基底 e1,e2,e3\boldsymbol{e_1},\boldsymbol{e_2},\boldsymbol{e_3} 作为正交基底，建立 空间直角坐标系 并用一个三元组 (x,y,z)(x,y,z) 作为坐标表示空间向量。

共面向量基本定理​

如果存在两个不共线的向量 x,y\boldsymbol{x},\boldsymbol{y}, 则向量 p\boldsymbol{p} 与 x,y\boldsymbol{x},\boldsymbol{y} 共面的充要条件是存在唯一实数对 (a,b)(a,b) 使得 p=ax+by\boldsymbol{p}=a\boldsymbol{x}+b\boldsymbol{y}。

方向向量​

空间直线的方向用一个与该直线平行的非零向量来表示，该向量称为这条直线的一个方向向量。直线在空间中的位置，由它经过的空间一点及它的一个方向向量 完全确定。

注意，平面中的直线也有方向向量。

对于 空间 中的直线，对其方向向量有以下求法：

  • 若有 A(x1,y1,z1),B(x2,y2,z2)A(x_1,y_1,z_1),B(x_2,y_2,z_2)，则 ABAB 所在直线的一个方向向量为 s=(x2−x1,y2−y1,z2−z1)\boldsymbol{s}=(x_2-x_1,y_2-y_1,z_2-z_1)。
  • 若已知一个与所求直线 垂直 的平面，该平面一般方程为 ax+by+cz+d=0ax+by+cz+d=0，那么垂直于该平面的直线的一个方向向量为 s=(a,b,c)\boldsymbol{s}=(a,b,c)，该方向向量也是该平面的 一个法向量。

法向量​

对于一个面 ABCDABCD，其法向量 n\boldsymbol{n} 与这个面垂直。

计算方法：任取两个面内直线 AB→,AD→\overrightarrow{AB},\overrightarrow{AD}，使得 AB→⋅n=0\overrightarrow{AB} \cdot \boldsymbol{n}=\boldsymbol{0} 且 AD→⋅n=0\overrightarrow{AD} \cdot \boldsymbol{n}=\boldsymbol{0}，利用坐标法即可计算。

扩展​

向量与矩阵​

矩阵运算的相关法则与向量运算相似，于是考虑将向量写成矩阵形式，这样就将向量问题化为矩阵问题了。详细内容请参考线性代数。

向量旋转​

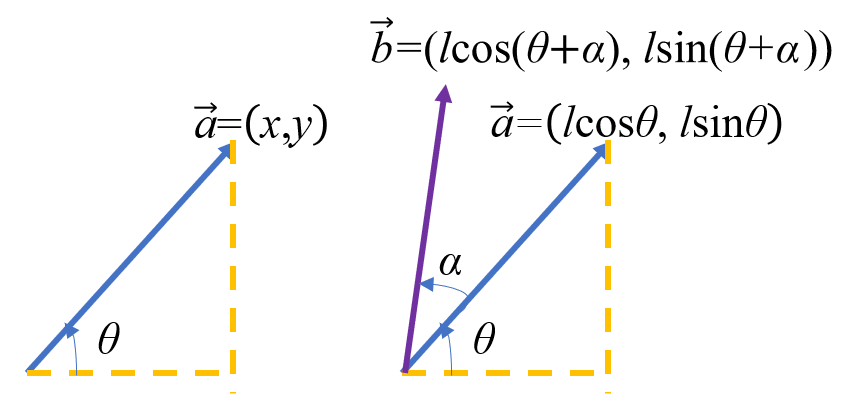
设 a=(x,y)\boldsymbol a=(x,y)，倾角为 θ\theta，长度为 l=x2+y2l=\sqrt{x^2+y^2}。则 x=lcos⁡θ,y=lsin⁡θx=l\cos \theta,y=l\sin\theta。令其逆时针旋转 α\alpha 度角，得到向量 b=(lcos⁡(θ+α),lsin⁡(θ+α))\boldsymbol b=(l\cos(\theta+\alpha),l\sin(\theta+\alpha))。

由三角恒等变换得，

b=(l(cos⁡θcos⁡α−sin⁡θsin⁡α),l(sin⁡θcos⁡α+cos⁡θsin⁡α))\boldsymbol{b}=(l(\cos\theta\cos\alpha-\sin\theta\sin\alpha),l(\sin\theta\cos\alpha+\cos\theta\sin\alpha))

化简，

b=(lcos⁡θcos⁡α−lsin⁡θsin⁡α,lsin⁡θcos⁡α+lcos⁡θsin⁡α)\boldsymbol b=(l\cos\theta\cos\alpha-l\sin\theta\sin\alpha,l\sin\theta\cos\alpha+l\cos\theta\sin\alpha)

把上面的 x,yx,y 代回来得

b=(xcos⁡α−ysin⁡α,ycos⁡α+xsin⁡α)\boldsymbol b=(x\cos\alpha-y\sin\alpha,y\cos\alpha+x\sin\alpha)

即使不知道三角恒等变换，这个式子也很容易记下来。