好高级的名字!
基本介绍
我们在初二就学习了一次函数及其应用,也就是 f(x)=kx(k=0)。虽然当时没讲,但是这里 k 所表示的就是这个函数的斜率,我们可以轻松的理解随着这个值的增大,函数也逐渐变陡,即斜率更大。
一次函数的变化是线性的,但是对于二次函数来讲,它的变化并不是,那我们又该如何去衡量这个变化率?
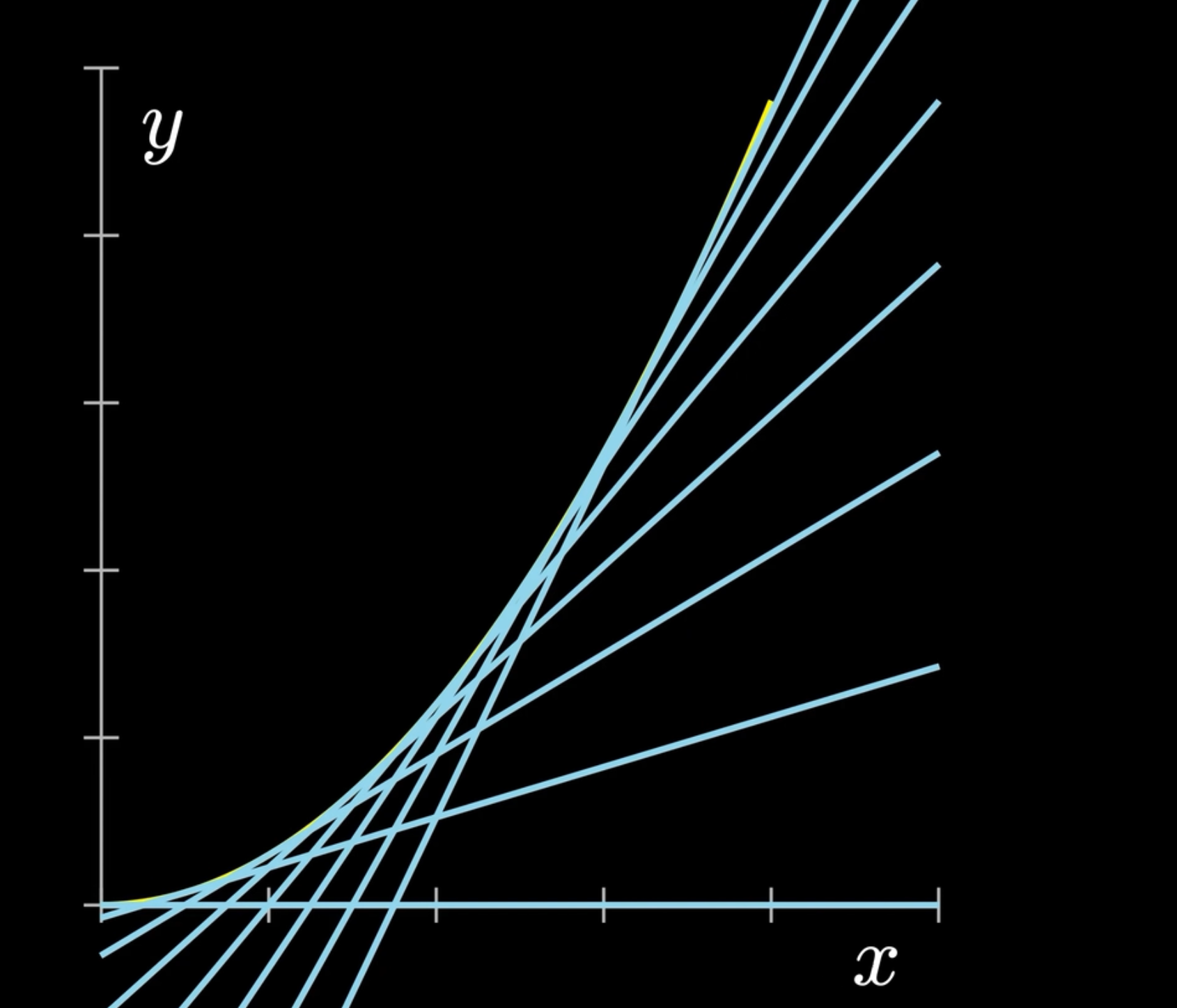
如图所示,我们对函数线上的每一个点去做切线,对于每一条切线,切线的斜率是越来越大的,这样一来我们便可以引出导数的概念。
点斜式求一次函数斜率
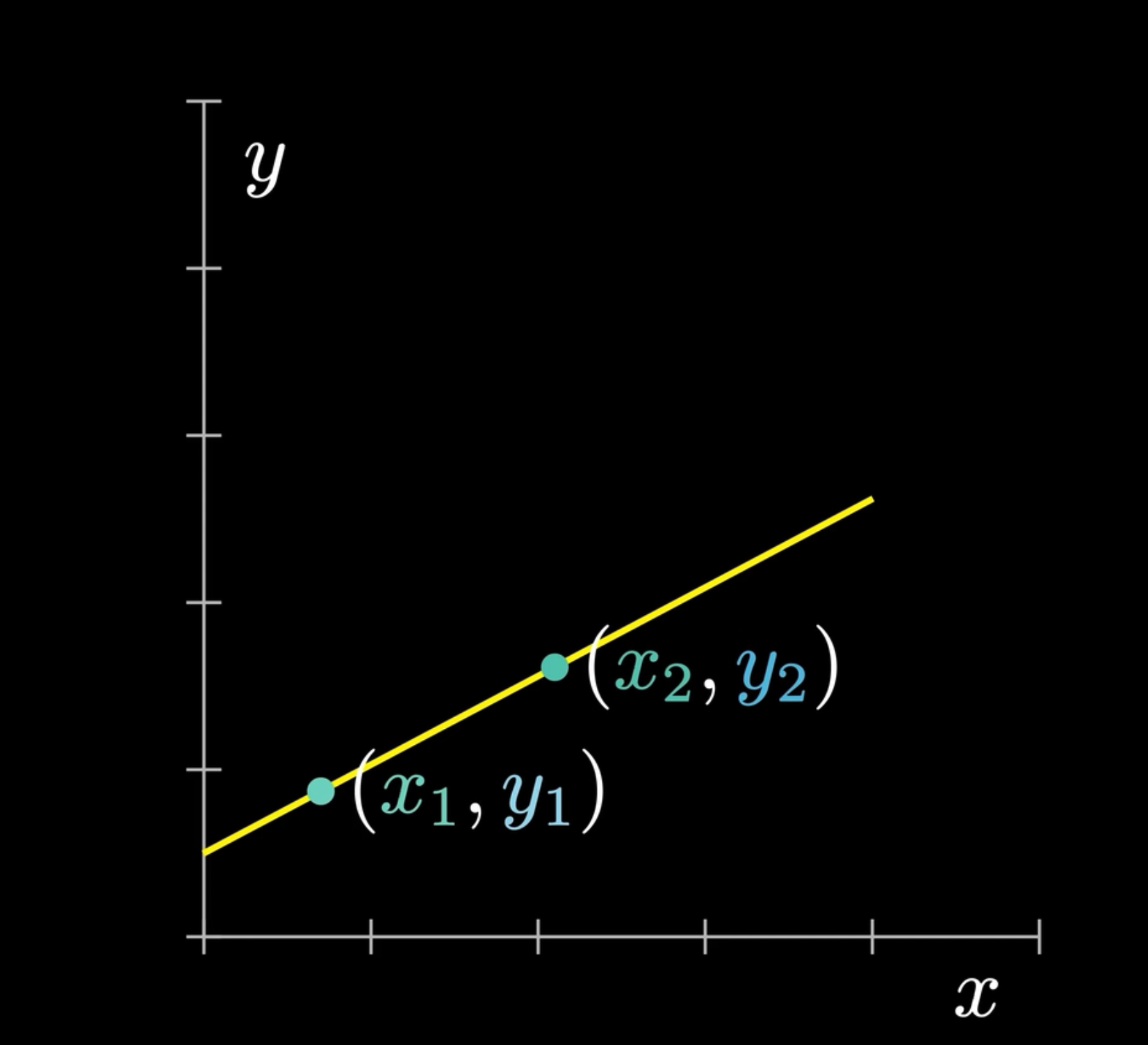
如图,我们在一个一次函数上找到两点:
(x1,y1),(x2,y2)
两个点的表达式可以写为:y1=kx1+b 和 y2=kx2+b。变形: y1−y2=k(x1−x2),可得:
k=x1−x2y1−y2
这个就是求斜率的简单公式,可以读出一次函数的斜率就是两点的横纵坐标之差作商,那么如何同样地去表达二次函数的“抛物线”呢?其切线又该如何去求?因此我们就引出导数的概念。
重要的概念 / 笔记 1
假设函数 y=f(x) 在点 x0 处有定义当自变量 x 在 x0 处取得增量 Δx相应的增量取得 Δy 如果 ΔxΔy 在 Δx→0时的极限存在,那么 y=f(x) 在 x0 处可导。
这确实有点令人头疼,不过我们可以简化为一个公式(你应当看过讲述极限那一章):
f′(x)=Δx→0limΔxf(x0+Δx)−f(x0)
我们仍然可以观察到 f(x0+Δx)−f(x0) 其实就等于 Δy,于是可以写成 f′(x)=Δx→0limΔxΔy。其实分数部份和点斜式法公式是等价的,即 ΔxΔy=x1−x2y1−y2=k=f′(x)。
运用一下
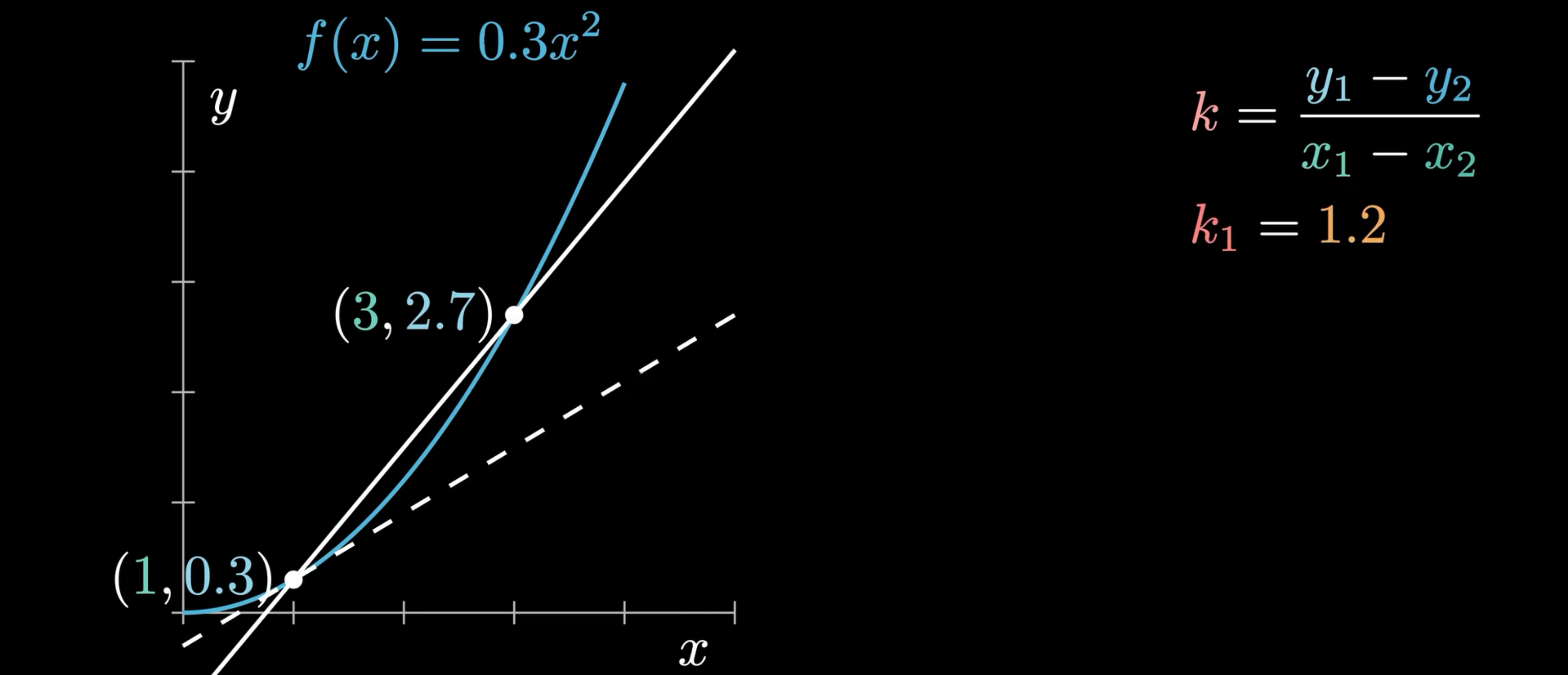
如图所示,我们需要知道虚线的切线斜率,但是我们只知道一个点,无法直接求出,那我们就引入另外一条经过抛物线两个点的切线,其中抛物线的表达式为 f(x)=0.3x2。根据点斜式公式,我们可以求出经过这两点的切线的斜率 k1=1.2。
然后,将两点之间的横纵坐标之差设为 Δx,Δy,我们发现,当两点相距越来越近的时候,过这两点之间的斜率也越来越趋近于这根切线的斜率。
幂函数求导公式,直接记就可以了,降幂打击,然后把幂次乘到系数里面。
我们可以比较轻松地得到这根切线的斜率:
k=Δx→0lim0.3Δx+0.6x这个是化简后的式子。
因此我们可以得出这根切线的斜率为 0.6。
Δx=0 是这个地方需要注意的,因为我们运用到了极限思想。它永远都是一个无限小的量,只不过是无限趋于 0。
承上启下
我不如将导数理解为某点附近的曲线变化率,但是如何从 f(x) 转换为 f′(x),接下来会继续讲。
求导运算
我们设有一个函数 f(x)=y=x2+2x+1,它对应的导函数 f′(x)=2x+2,至于是怎么得来的,我们稍后再讲。
那么一条切线经过 x=1 且经过这个二次函数的斜率 k=2∗1+2=4,你也可以代入更多的值。代入更多的值我们发现,导函数所表示的值就是在该点处切线的斜率 k 的值。因此我们可以得出如下的结论:
- 当 f′(x)>0 时,所在的点的切线斜率 k 就大于 0,所以这条切线是随横坐标的增加而增加的。
- 当 f′(x)<0 时,所在的点的切线斜率 k 就小于 0,所以这条切线是随横坐标的增加而减小的。
了解了上述的性质之后,我们来看看基本求导公式:
(C)′=0(C∈R)(axα)′=aαxα−1(lnx)′=x1(ex)′=ex(ax)′=axlna(sinx)′=cosx(cosx)′=−sinx如果这个常数前面有一个系数,比如第二个,变化的时候直接在前面加上系数即可,系数不变,同理第三个如果 lnx 前面有一个系数 a,那么对应的导函数就是 xa。
所以你知道了 f(x)=x2+2x+1 是如何转化了吧。因此,我们又可以知道,与 f(x)=ax2+bx+c 对应的导函数 f′(x)=2ax+b。我们知道二次函数的顶点处所做的切线的斜率为 0,即这根切线与 x 轴重合,所以这个地方的横纵标为 −2ab,千万不要看不懂,学了直线和方程以及一次函数就可以懂了(虽然只是一个大概)。
大总结
好了,本章结束了,虽然只讲了一点,涵盖了概念和求导的公式,但是真正的内容还很长很长,这或许会对我们在一次函数的练习题有一点整活的余地~



